3.1 – Derivative of a Function

Slopes

From section 2.4, we know that the function to calculate the slope of a line can be found using the formula

$$m=\underset{h\to 0}{\lim }\frac{f(a+h)-f(a)}{h}$$

In this above formula, $a$ represents the point at which we want to find the slope, and $h$ is an infinitesimally small distance away from $a$.

Definition of the Derivative

For some continuous and differentiable $f(x)$ at $x$, the derivative $f^{\prime }(x)$ is equal to

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

or alternatively at $x=a$,

$$f^{\prime }(a)=\underset{x\to a}{\lim }\frac{f(x)-f(a)}{x-a}$$

Examples

The derivative of $f(x)=x^2-4$ at $x=3$:

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{(x+h{)}^2-4-(x^2-4)}{h}$$ $$=\underset{h\to 0}{\lim }\frac{x^2-2xh-h^2-4-x^2+4}{h}$$ $$=\underset{h\to 0}{\lim }\frac{h(2x-h)}{h}$$ $$=\underset{h\to 0}{\lim }2x-h$$ $$=2x-0$$ $$f^{\prime }(x)=2x$$

Therefore,

$$f^{\prime }(3)=2(3)$$ $$f^{\prime }(3)=6$$

The derivative of $f(x)=\sqrt{x}$ at $x=a$:

$$f^{\prime }(a)=\underset{x\to a}{\lim }\frac{\sqrt{x}-\sqrt{a}}{x-a}$$ $$=\underset{x\to a}{\lim }\frac{\sqrt{x}-\sqrt{a}}{x-a}\cdot \frac{(\sqrt{x}+\sqrt{a})}{(\sqrt{x}+\sqrt{a})}$$ $$=\underset{x\to a}{\lim }\frac{(x-a)}{(x-a)(\sqrt{x}+\sqrt{a})}$$ $$=\underset{x\to a}{\lim }\frac{1}{\sqrt{x}+\sqrt{a}}$$ $$=\frac{1}{\sqrt{x}+\sqrt{x}}$$ $$=\frac{1}{2\sqrt{x}}$$

Relating $f$ and $f^{\prime }$

A horizontal line $y=1$ has a slope of zero. It follows that the derivative $y^{\prime }$ would be equal to zero.

For a other differentiable functions that are not completely horizontal throughout their domains, points where the slope is equal to zero are the roots of the derivative.

These zero points are local minima and maxima, where $f$ reaches a peak or trough. To find minima and maxima, identify the roots of the first derivative $f^{\prime }$.

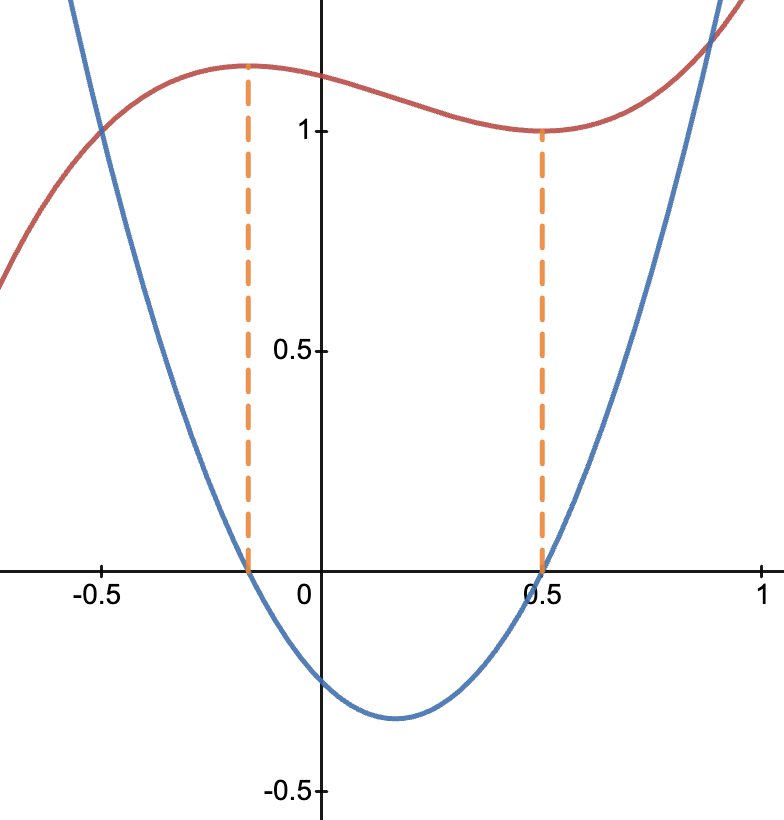A graphical representation

Tangent Lines

The derivative $f^{\prime }(x)$ at any point $a$ in the domain of $f(x)$ is equal to the slope at $f(a)$.