Chapter 3 – Probability

Terminology

• Experiment: a planned operation carried out under controlled conditions

  • Chance experiment: outcome is not predetermined (flipping a fair coin)
  • Outcome: the result of an experiment
  • Sample space: all possible outcomes (sample space of a D6 = {1, 2, 3, 4, 5, 6})
  • Event: any combination of outcomes

• Long-term relative frequency: the probability of any outcome

  • Probabilities are between 0 and 1 (inclusive)

• Equally likely: each outcome occurs with equal probability

• Law of large numbers: the empirical (observed) relative frequency of an outcome tends to the its theoretical probability over a large number of repetitions

Notation for Probability

• $P(A)$: outcomes $A$
• OR $P(A\cup B)$: outcomes $A$ OR $B$ or both
• AND $P(A\cap B)$: outcomes $A$ AND $B$
• Complement $P(A^{\prime })$: all outcomes NOT in $A$ $(P(A)+P(A^{\prime })=1)$
• Conditional $P(A|B)$: $A$ given $B$ $(\frac{P(A\cap B)}{P(B)},P(B)>0)$

Probability	Venn Diagram
$P(A)⠀⠀⠀⠀⠀$
$P(A\cup B)$
$P(A\cap B)$

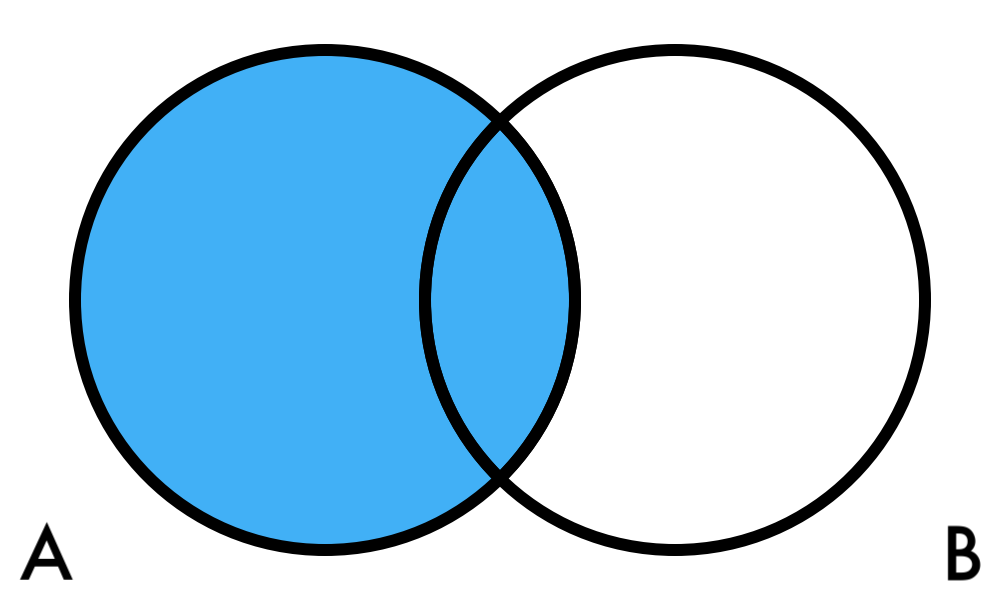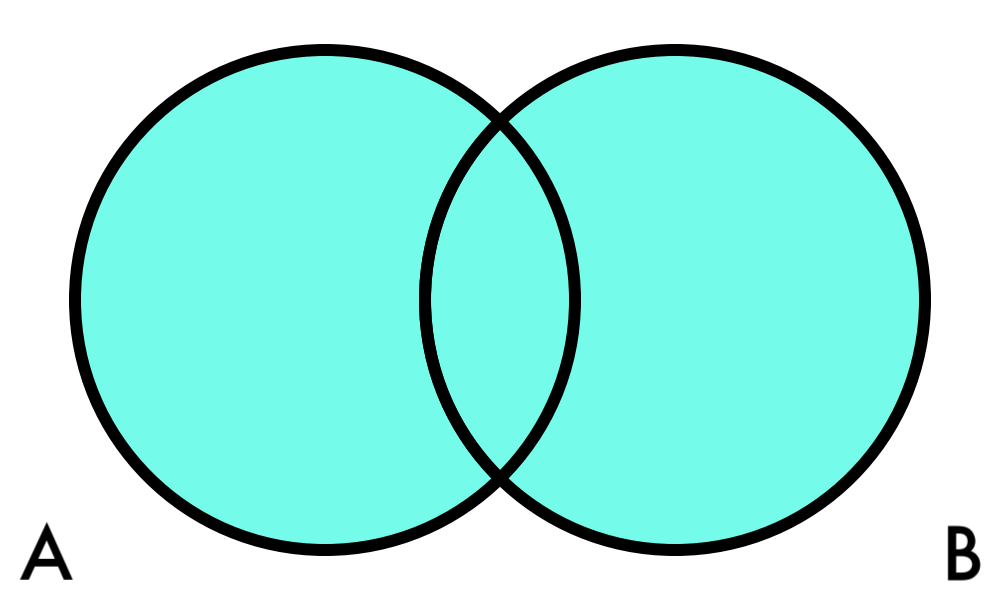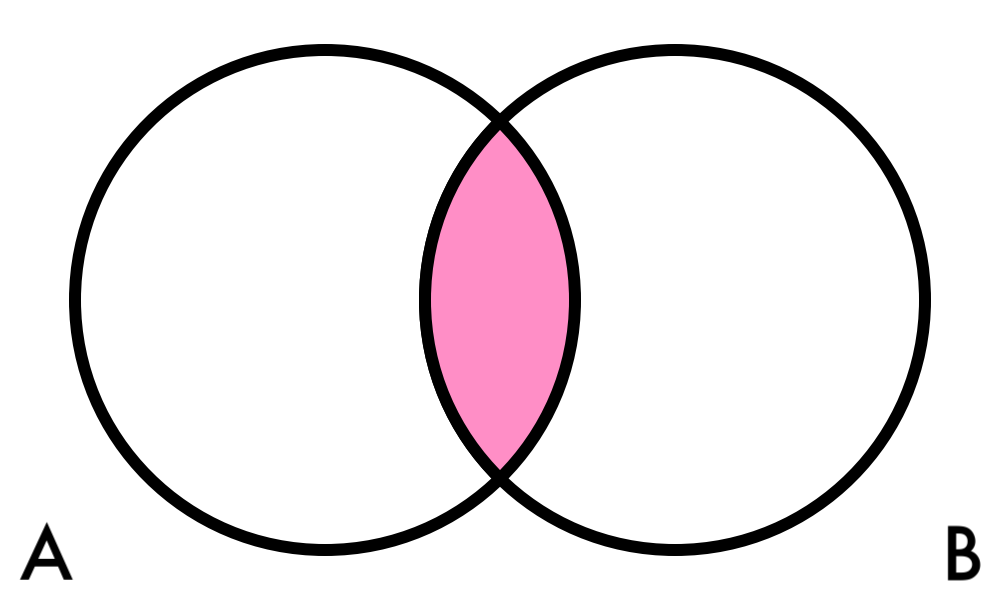Independent and Mutually Exclusive Events

Independent Events

Two events are independent if:

• $P(A|B)=P(A)$
• $P(B|A)=P(B)$
• $P(A\cap B)=P(A)P(B)$

This simply means that knowledge of one event will not affect the other.

$$P(A\cap B)=P(A)P(B)⟺P(A|B)=\frac{P(A\cap B)}{P(B)}=P(A)$$ $$P(A|B)=\frac{P(A)\cancel{P(B)}}{\cancel{P(B)}}=P(A)$$

Assume events are dependent until proven otherwise.

Mutually Exclusive Events

Two events are mutually exclusive if:

• $P(A\cap B)=0$

This means they cannot occur at the same time. Assume events are not mutually exclusive until proven otherwise.

Two Basic Rules

Multiplication Rule

• $P(A\cap B)=P(B)P(A|B)$
• $P(A|B)=\frac{P(A\cap B)}{P(B)}$

When $A$ and $B$ and are independent:

• $P(A\cap B)=P(A)P(B)$

Addition Rule

• $P(A\cup B)=P(A)+P(B)-P(A\cap B)$

When $A$ and $B$ are mutually exclusive:

• $P(A\cup B)=P(A)+P(B)$

Contingency Tables

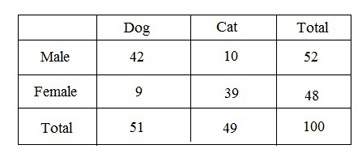• Examples:
  • $P(\text{Male}|\text{Dog})=\frac{42}{51}\approx 0.824$
  • $P(\text{Female}\cap \text{Cat})=\frac{39}{100}=0.39$

Tree and Venn Diagrams

Tree Diagrams

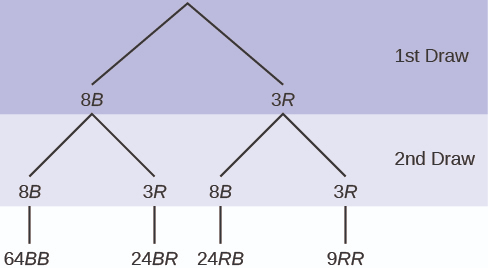(with replacement)

The final stage of the tree diagram represents the frequencies of all outcomes, which are out of 121 (64 + 24 + 24 + 9 = 121).

• Examples:
  • $P(RR)=\frac{9}{121}\approx 0.0744$
  • $P(RB\cup BR)=\frac{24+24}{121}\approx 0.397$
  • $P(R_2|B_1)=\frac{24/121}{8/11}\approx 0.273$ ( also calculated as $\frac{24}{88}$ from the reduced sample space)

Venn Diagrams

• $A=\{1,2,3,4,5\}$

• $B=\{7,8,9\}$

• $A\cap B=\{6\}$

• $A\cup B=\{1,2,3,4,5,6,7,8,9\}$

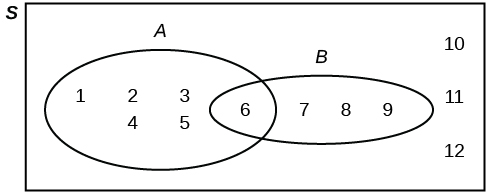• Examples:

  • $P(A\cup B)=\frac{9}{12}=0.75$
  • $P(B|A)=\frac{1}{6}\approx 0.167$

Example

2% of a population of dogs have a disease. There is a test dogs can take for the disease. If a dog has the disease, the test will have a positive result 95% of the time. If the dogs does not have the disease, the test will have a positive result 12% of the time.

What is the probability a dog has a positive test?

$P(\text{D})=0.02$ $P(\text{N})=0.98$

$P(D_{+})=0.95$ $P(N_{+})=0.12$

$P(+)=P(D\cap D_{+})+P(N\cap N_{+})$ $P(+)=[P(D)][P(D_{+})]+[P(N)][P(N_{+})]$ $P(+)=[0.02][0.95]+[0.98][0.12]=0.1366$

Give that a dog tests positive, what is the probability that it actually has the disease?

$P(D|+)=\frac{P(D\cap D_{+})}{P(+)}$ $P(D|+)=\frac{[0.02][0.95]}{0.1366}=0.1391$