Demonstrating the Monty Hall Problem in Python

Imagine you are a contestant on a game show where behind one of three doors is a car, each door equally likely to contain the car.

The host opens one of the other two doors that you didn’t choose, revealing that it contained nothing, offering you the option of switching to the other remaining door.

Consider the initial probability $\text{P}(\text{my door})$ that your door contains the car:

$$\text{P}(\text{my door})=\frac{1\text{door}}{3\text{doors}}=33.33\%$$

And the probability that the other two doors you didn’t pick contain the car:

$$\text{P}(\text{other doors})=\frac{2\text{doors}}{3\text{doors}}=66.66\%$$

Think about this problem for a second. Consider these two pieces of information:

1. The two doors that you didn’t select have a combined probability of 2/3rds
2. One of the two that you didn’t select must contain no car, since there’s only one car

Now ask yourself if it matters that the host revealed which door had no car with absolute certainty – because it really shouldn’t.

We knew from the beginning that one must have been empty, but that didn’t change our initial probability estimate. By offering you the option to switch, the host is really giving you the chance to increase your odds from 1/3rd to 2/3rds!

Simulation

This problem is famous for not being so intuitive, so we can employ a Monte Carlo simulation in Python to experimentally determine if our above assumptions are correct. We do this by writing a program that randomly selects which door contains the car, and randomly selects a door to open.

def sample(trials: int, switch: bool) -> float:
	success = 0

	for _ in range(trials):
		car = random.randint(0, 2)
		choice = random.randint(0, 2)
	
		if switch:
			hint = next(i for i in range(3) if i != choice and i != car)
			choice = 3 - choice - hint
		
		if choice == car:
			success += 1
		
	return success / trials

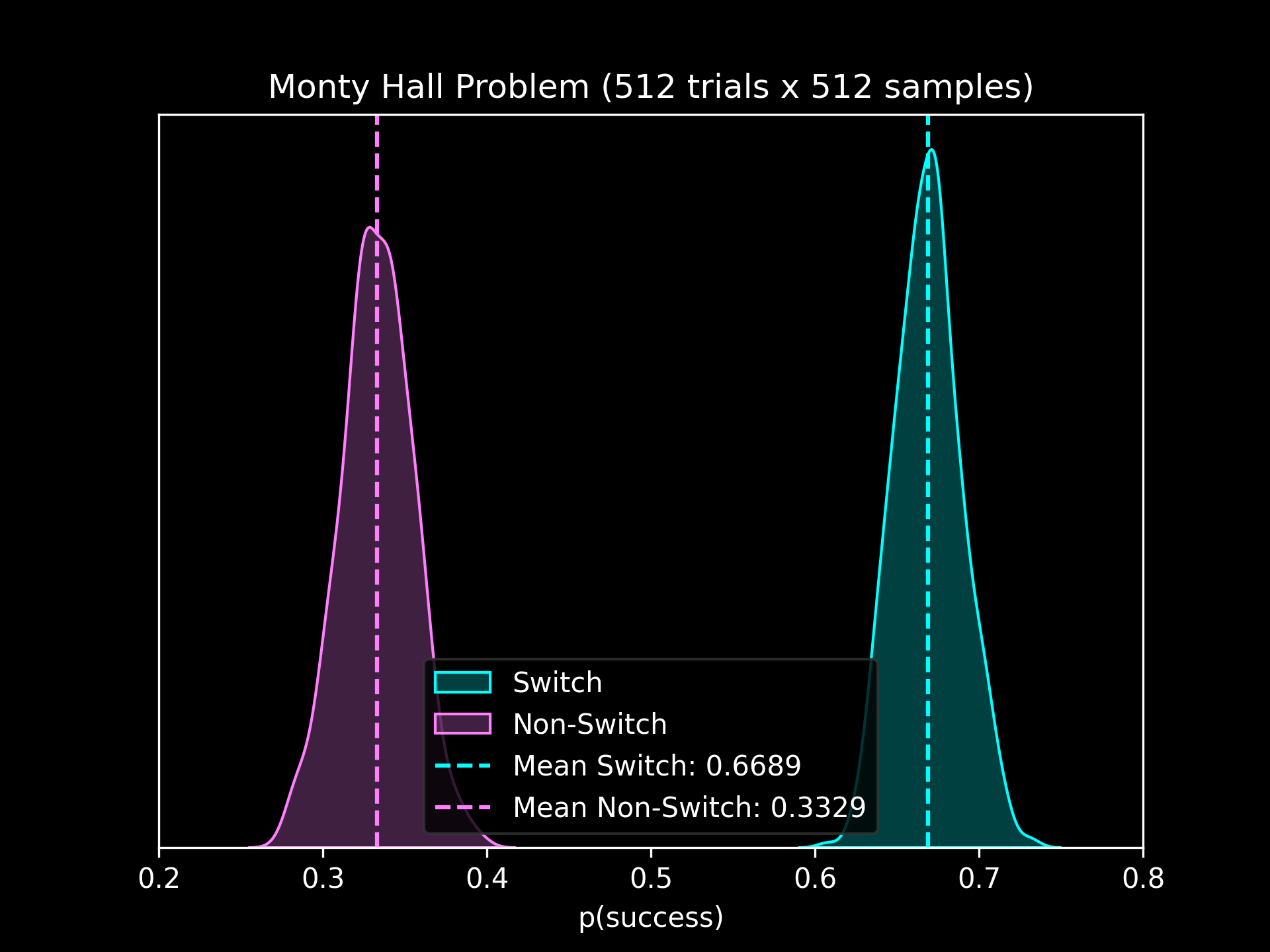
sample returns the odds that the correct door was chosen over $\text{n}$ trials, considering if we chose to switch or not. Plotted over 512 samples of 512 trials:

We find that the probability of choosing correctly is ~33% when not switching and ~67% when switching.